História

Paul Drude (1863 – 1906)
Após a descoberta do elétron, pelo físico Joseph John Thomson, em 1897, utilizando os raios catódicos, a comunidade científica, alguns anos à frente, se deparou com o início do desenvolvimento da teoria quântica. Assim, os físicos estavam buscando estudar o estado sólido da matéria, explicando os fenômenos ocorridos nos materiais. Durante esses estudos, o físico alemão Paul Drude (1863- 1906), propôs um modelo que explica a condução elétrica dos metais.
O Modelo
"Drude considerou que quando há átomos unidos formando um material metálico, os elétrons da última camada se desprendem e se tornam livres, equanto os íons permanecem fixos. A teoria consistiu em supor um gás de elétrons e utilizar conceitos provenientes da teoria cinética dos gases a fim de simplificar o modelo. Aqui, os elétrons são com esferas rígidas, e idênticas, as quais se movem entre os íons e eventualmente se chocam com eles. Aos elétrons livres citados a pouco dá-se o nome de elétrons de condução." (AMORIM) Para a formulação do modelo, Drude considerou 4 hipóteses, sendo elas:
● Não existe interação elétron – elétron;
● As colisões ocorrem de forma inesperada, de forma que não exista movimento dos íons;
● Existe um tempo médio entre as colisões;
● O elétron perde a memória sobre a trajetória e velocidade, após cada colisão.
Agora considerando um condutor, em equilíbrio eletrostático, temos algumas observações:
● O campo elétrico é nulo em seu interior, logo não existe corrente elétrica;
● Mesmo não existindo corrente elétrica, existe um movimento de elétrons no interior do condutor. Esse movimento se equipara ao movimento das moléculas de um gás ideal. O movimento ocorre de forma aleatória com uma velocidade muita alta, da faixa de 106m/s;
● Os elétrons são atraídos pelos íons, assim não escapam do material;
● O movimento é caótico, logo não existe um fluxo efetivo em nenhuma direção, não existindo corrente elétrica.
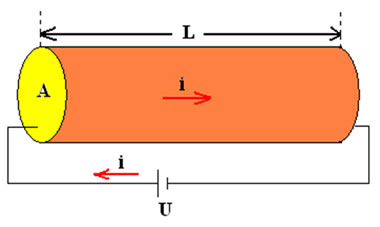
Na existência de um campo elétrico, existe um movimento de arraste provocado pelo campo. Esse movimento é na direção da força elétrica 𝐹⃗ e tem uma ordem de grandeza de aproximadamente 10-4m/s. Como existe um movimento de arraste, há também uma velocidade de arraste 𝑣⃗, a qual provoca um arraste ordenado das cargas, em um sentido determinado, no condutor. Essa movimentação de cargas é denominada: corrente elétrica. A corrente elétrica (i) por unidade de área transversal (A) define o módulo do vetor densidade de corrente (J). $$ {J=\frac{i}{A} \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space (1)} $$ Já a corrente elétrica é definida como o fluxo total das cargas (Q) por unidade de tempo (Δt). Sendo basicamente expressada como: $$ {i=\frac{Q}{\Delta t} \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space (2)} $$
Sentido, Direção e Condutividade
Sentido e Direção da Corrente Elétrica
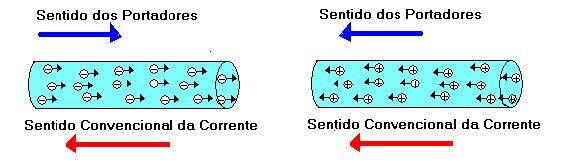
Com a movimentação de cargas em uma determinada direção, é esperado que exista um sentido para a corrente elétrica. Mas como determinar o sentido dessa grandeza a partir da sua carga? Se o movimento for de prótons, como no acelerador de partículas, por exemplo, haverá a movimentação de cargas positivas. Já no caso da corrente elétrica gerada nos condutores usuais, o que ocorre é o arraste de elétrons. Desse modo, o sentido convencional adotado é dado ao observar o movimento dos portadores de carga, atribuindo-o conforme o sentido teórico ou real de cargas positivas. Nesse sentido, se a corrente elétrica for gerada por prótons, é adotado o sentido real dessa movimentação. Todavia, se a corrente é produzida por elétrons, o sentido covencional é adotado pelo movimento teórico de cargas positivas. Veja a imagem abaixo:
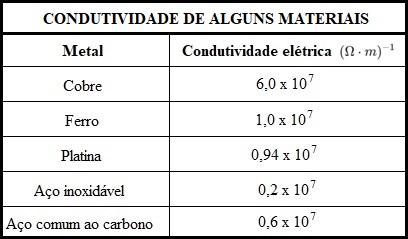
Condutividade
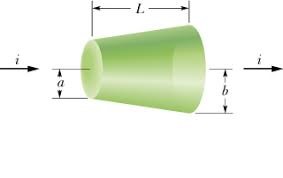
Já a condutividade elétrica de um material representa a capacidade que ele tem de transportar cargas elétricas, quando submetido a uma diferença de potencial. Um material de condutividade alta tem uma facilidade de transportar cargas elétricas e, de maneira oposta, um material com condutividade elétrica baixa apresenta uma resistência maior ao transporte de cargas elétricas. A condutividade (σ) é dada pela razão entre a densidade de corrente (J) e o campo elétrico (E), tal que: $$ { \sigma = \frac{J}{E} \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space (3.1)} $$ Ainda mais, a condutividade (σ) também pode ser expressa como: $$ { \sigma = \frac{n \cdot e^2 \cdot \tau}{m} \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space (3.2)} $$
Fatores que Afetam a Condutividade
A condutividade não é uma propriedade constante na natureza, ela varia entre um condutor e outro, além de que pode ser alterada ou influenciada por alguns aspectos, tais como:
Temperatura
Ao aumentar a temperatura de um condutor, pode-se alterar sua condutividade, tendo em vista que essa variação ocorre em virtude da excitação térmica dos átomos dos materiais. Não é atoa que alguns aparelhos eletrônicos sensíveis costumam ser acompanhados de mecanismos de resfriamento para manter a temperatura do condutor constante. Por exemplo, o cooler em um notebook, que tem o papel de reduzir o calor gerado pelos componentes da máquina.

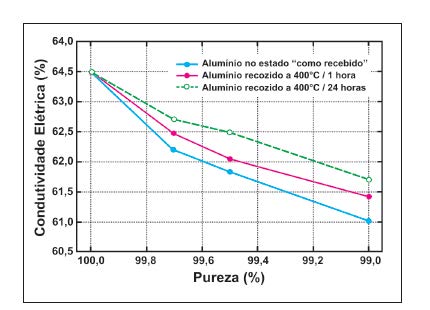
Impurezas
Ao se ter impurezas, ou seja, partículas de isolamento de elementos não condutores nos condutores elétricos, pode haver impedimento do fluxo de corrente nos condutores, levando a uma diminuição nos níveis de condutividade do material (essas partículas podem ser de origem natural ou por falhas de fabricação). Por exemplo, o nível de impureza em materiais semicondutores afeta a condutividade mais do que nos materiais condutores, em alguns casos melhorando-a e em outros casos reduzindo a condutividade. O gráfico ao lado mostra a relação da condutividade do alumínio e a quantidade de impurezas:
Frequência
Ao trabalhar com corrente alternada, ou seja, que oscila quando flui, pode haver interferência da frequência da corrente elétrica, uma vez que quando muito aumentada, acima de um certo limite, ocasiona em um fluxo de corrente no redor de um condutor e não através dele. Essa situação é também conhecida como efeito pelicular, que ocorre normalmente quando a frequência aumenta acima de 3GHz (ou 3.000.000.000 ciclos oscilatórios de corrente por segundo).
Campos eletromagnéticos
Ao constatar a presença de campos eletromagnéticos ao redor do condutor elétrico, sua condutividade pode ser alterada. Embora os condutores criem campos magnéticos quando conduzem corrente elétrica, esses campos se encontram de forma perpendicular uns aos outros, o que não causa problema no fluxo de corrente. Porém, quando se trata de campos externos, essa organização é independente, o que pode atrapalhar o fluxo de corrente ou até interrompê-lo, dependendo de sua intensidade.