Propriedades Eletrostáticas
Força Elétrica
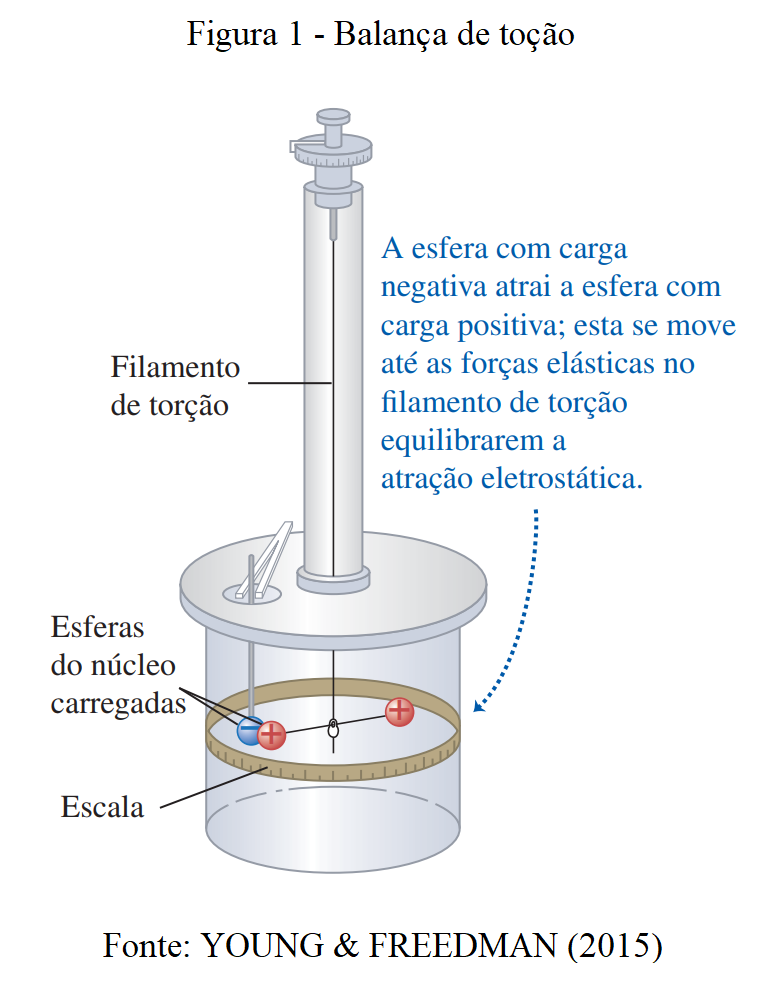
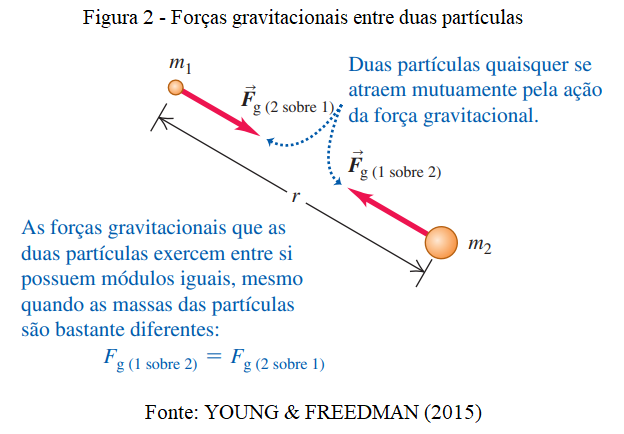
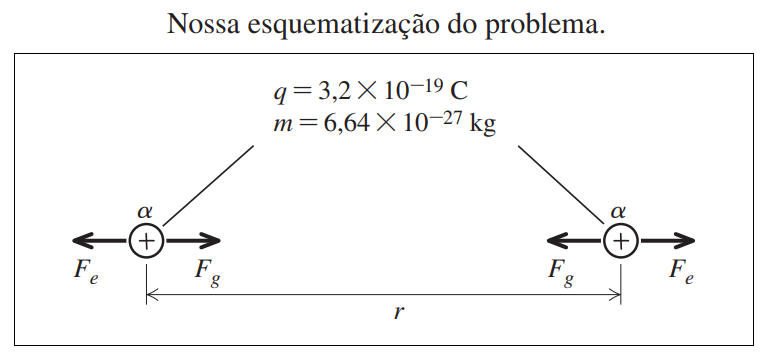
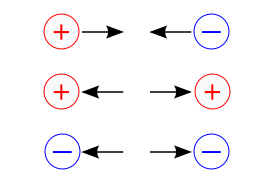
A força elétrica trata da interação de repulsão e atração dos corpos devido ao campo elétrico gerado por cada um deles. Como ilustrado, cargas com sinais iguais se repelem enquanto cargas com sinais diferentes se atraem.
Eletrização
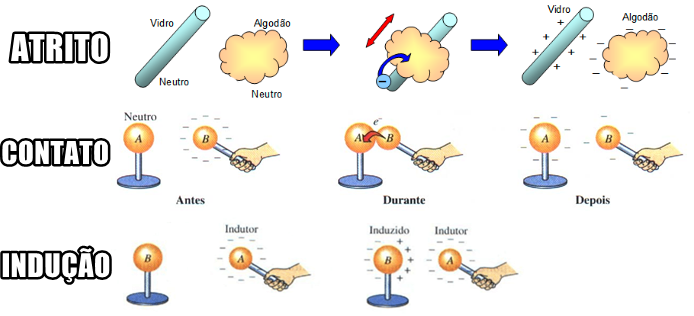
Consiste no processo de transformar um corpo inicialmente neutro em um corpo eletricamente carregado. Isso pode ser feito de três maneiras: atrito, contato ou indução.
Carga Fundamental
Representa o menor valor possível para uma carga existente, sendo atribuído aos prótons e elétrons. $$ {e=1,60217662 \cdot 10^{-19}C} $$
Quantização de Carga
Por definição, a quantização de uma carga elétrica é referente a multiplicação de um inteiro de uma carga fundamental, ou seja: $$ {Q=n \cdot e} $$